内容导读

  连续空间分布(spatial distribution)快照数据所体现的空间演化过程受到空间交互（spatial interaction）的驱动，挖掘隐藏在分布演化背后的交互模式有助于理解空间分异格局。本研究通过将大规模线性规划算法以及人类移动的空间约束进行整合，提出了一种基于连续空间分布反演空间交互模式的方法。该方法在推算中国春节期间城际返乡流的实验中取得了理想的实证结果，证明了基于离散的多时相人口空间分布数据推算空间交互模式的可行性。

 

作者简介

朱递

北京大学遥感与地理信息系统研究所博士生

研究方向：空间分异格局建模|时空统计|社会感知|深度学习

个人主页：https://www.researchgate.net/profile/Di_Zhu36

工作邮箱：patrick.zhu@pku.edu.cn

 

朱递，北京大学遥感与地理信息系统研究所博士生，北京大学唐立新奖学金获得者。本科毕业于北京大学地理信息系统专业，同时取得了北京大学国家发展研究院经济学学士学位。曾在Applied Geography、IJGIS等国内外知名期刊发表学术论文。

 

研究背景

    空间分异与空间交互在复杂的地理世界中是不可分割的两个现象。前者指位置之间有着互不相同的趋势，从而体现出某种属性在一阶空间分布上的异质性。而后者对应着发生在空间中的二阶移动过程，例如人流、货流、资金流等。一方面，分布的异质性能够导致交互模式的形成与演化，另一方面，空间交互也在不断塑造空间分异格局的过程中扮演着重要的作用。海量时空大数据的出现，为我们提供了探究二者动态关系的绝佳机遇。

    受到用户隐私保护、轨迹提取困难、数据量不足等因素的影响，在实际研究和应用中，高质量空间交互数据集的获取是非常困难的，更易获得的是连续时相的空间分布快照数据。而前人的工作集中于空间分布的描述、空间交互的建模以及基于空间交互模式的分异格局求解，缺乏从空间分布的演化推算空间交互模式的定量方法。

 

研究方法

    假设两个连续的空间分布快照之间只存在一种起主导驱动作用的空间交互模式导致了空间分布的演化，反演空间交互模式的策略与网络优化领域的最小成本流问题(minimum-cost flow problem)相类似。

构造与求解人口移动的线性规划问题

    为了从众多能够与观测到的分布演化吻合的空间交互模式中求解出最符合真实情况的模式，可以将问题构造为一个空间优化任务：在满足空间分布格局的演变和人类移动性特征的双重约束下，使交互的总成本最小。

 

   

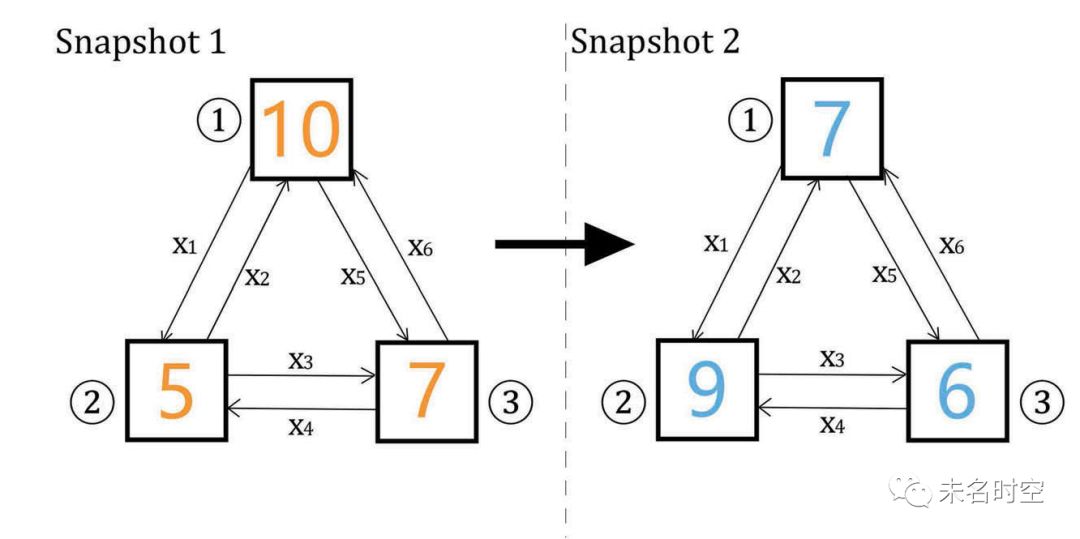
图 1 基于两个连续时相分布推算空间交互模式的一个简单示例

    以图一为例，共3个空间单元，两个时相的分布快照分别可以表达为[10,5,7]和[7,9,6]，反映交互模式的全连通网络可以表示为x=[x1,x2,x3,x4,x5,x6]。假设每两个空间单元之间产生交互的成本均为1，可以构造如下的线性规划问题：

 

   

 

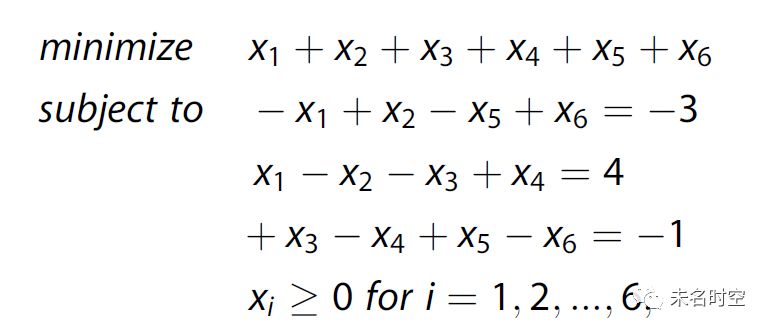
    运用高斯约当消元（Gauss-Jordan elimination），可以将上式改写为可以被单纯形法（simplex method）求解的如下标准形式（equational form）：

 

 

   

 

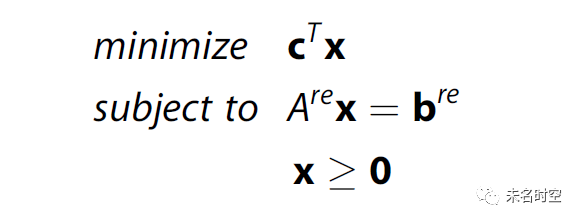
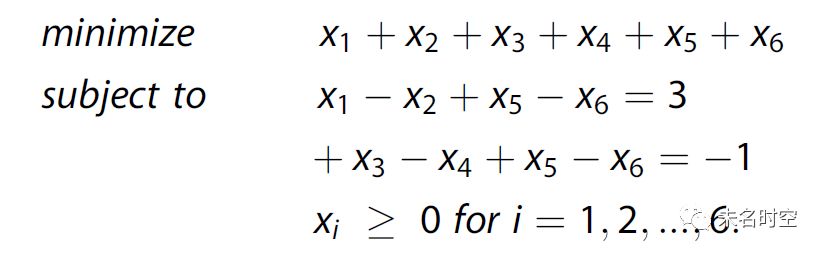
    其中，c是交互的成本矩阵，x是含有n个变量的向量，A^re是一个秩为m的规范行阶梯型(reduced row echelon form)矩阵，其列数n不小于行数m。通过迭代地构建单纯型表(simplex tableau)的方式，可以求出图1所示情况下的最优解为x=[3,0,0,1,0,0]，总成本为4。

    假设位置i与位置j之间发生空间交互的单位成本为c_i,j，而整个系统中空间交互的总成本为常量：

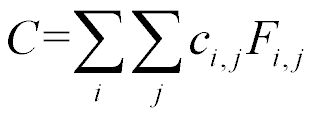
    将幂率衰减形式的空间交互重力模型代入，可以得到顾及人类移动性的空间交互成本：

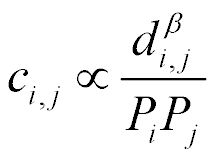
    其中，F为交互量，P为吸引力，d为欧式距离。这种定义方式可以得到更加符合边际成本递减认知的非线性空间交互成本，即：

 

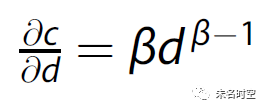
  因此，基于以上可以构建从连续空间分布快照求解空间交互模式(Inferring Interactions from Distribution Snapshots, IIDS）的方法：

  1）假设在n个空间单元构成的研究范围内，t1和t2时刻的人口分布分别为

 

 

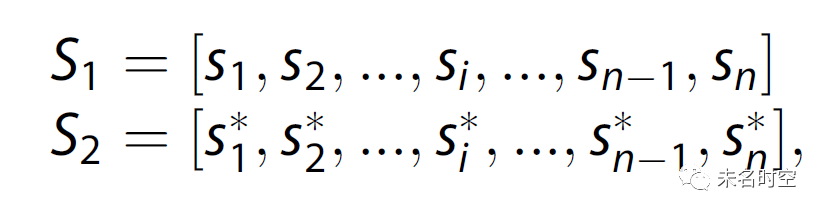
  2）全连通的空间交互矩阵为

 

   

 

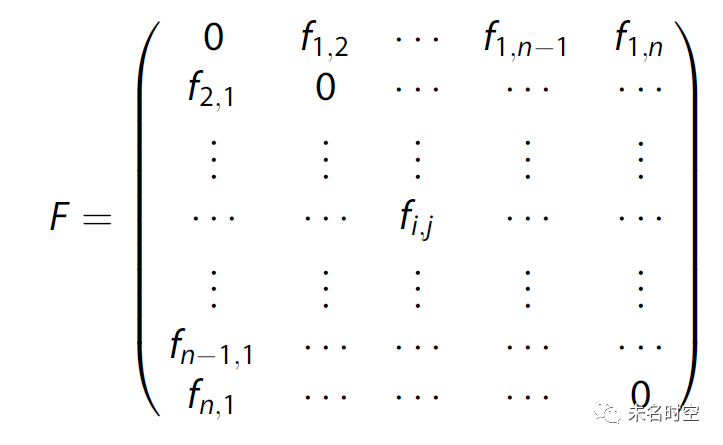
  3）对应的成本矩阵为

 

   

 

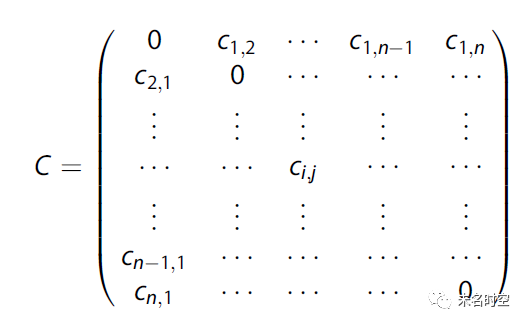
  4）待求解的线性规划问题为

 

   

 

   

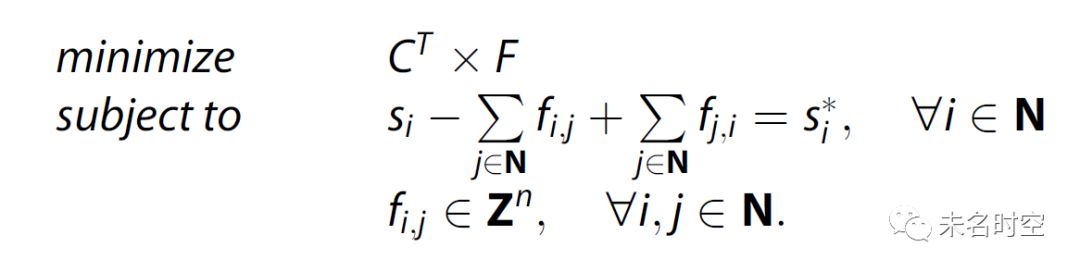
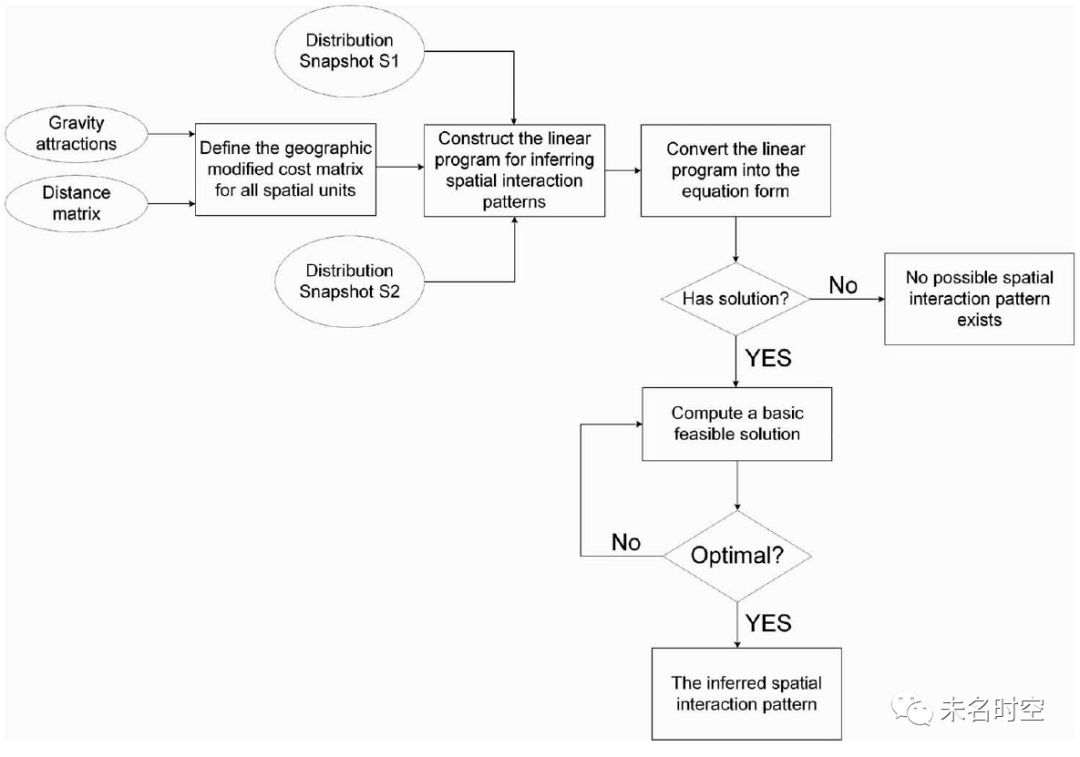
图 2 基于分布快照推算交互模式（IIDS）的流程图，成本矩阵的定义可以根据实际场景进行调整

 

模拟实验

    本研究提出的基于连续分布快照推算交互模式（IIDS）的方法在四个简单模拟场景下的实验结果如图3所示。

 

   

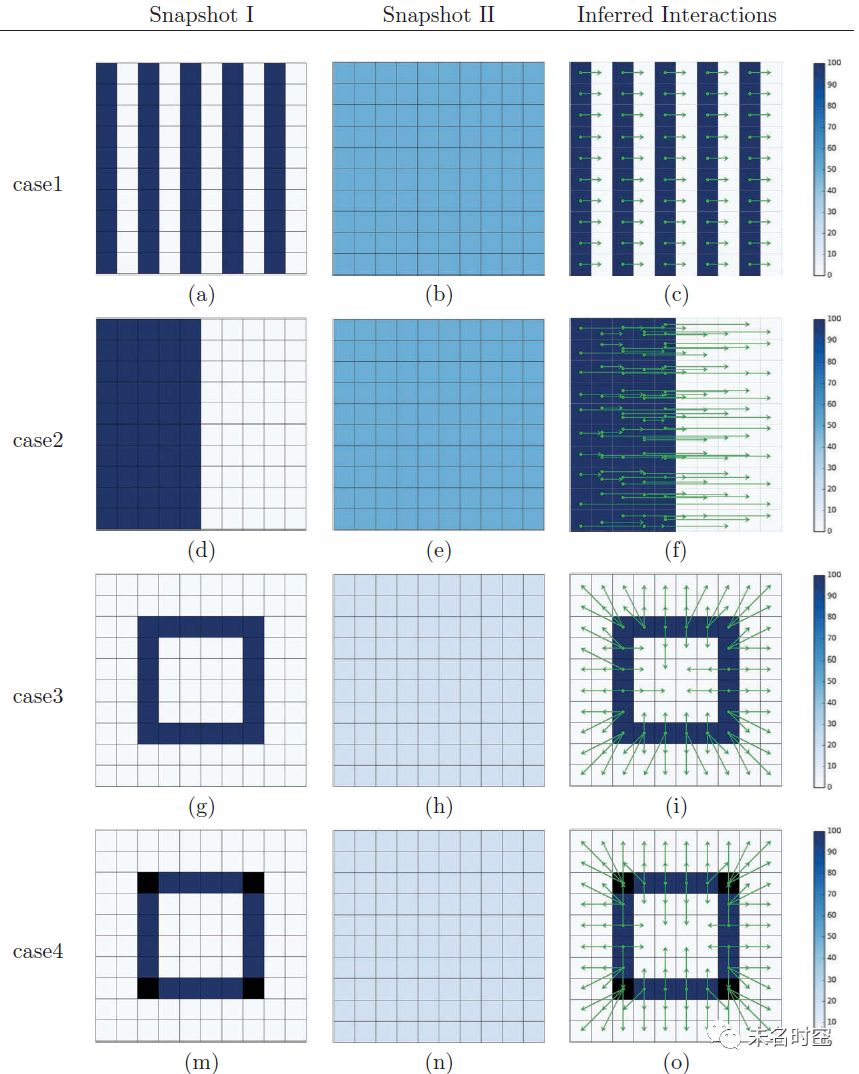
图 3 模拟场景下的实验结果

 

    四个初始的空间分布全部演化为了均匀分布，由于这四个简单场景下的真实空间交互模式可以通过直观地推测得到，我们可以通过发现IIDS方法的一些特点。

  Case1:斑纹状的分布演化为均匀分布，分布总量不变。假设格网吸引力相同，成本按照距离倒数计算。图3(c)所示结果明显是该情况下的最优解，50个等权重的距离为1的空间交互可以导致图3(a)到3(b)的演化。

  Case2:斑纹状的分布演化为均匀分布，分布总量不变。假设格网吸引力相同，成本按照距离倒数计算。图3(f)所示结果中10行共72个交互，每一行推算结果模式不一致，但成本相同。也就是说，IIDS会从等价的最优解中随机挑选一个作为输出。

 Case3:环状的分布演化为均匀分布，分布总量不变。假设格网吸引力相同，成本按照距离倒数计算。图3(i)所示结果中左上四分之一区域的交互模式与另外三个区域略有差异，而每个区域内的总成本一致，原因与Case2相同。

 Case4: 环状的分布演化为均匀分布，分布总量不变。四个黑色格网具有100倍的吸引力，成本按照重力模型进行计算。可以看到图3(o)相比

Case3的结果进行了重新分配，出现了非零值格网之间的交互，同时在每个四分之一区域呈现出稳定的唯一最优解。在实际情况中，由于吸引力的分布比较复杂（例如人口分布），IIDS一般均会得到唯一的输出。

 

实证研究

 

数据描述

   

图 4 春节前(2016.1.18-1.22)与春节时(2016.2.7-2.11)两个时相的日均分布数据

 

    数据集是腾讯移动端应用采集到的全国定位数据，包含了从2016年1月16日至2月12日连续28天在全国每个0.01°* 0.01°地理经纬度格网中的活跃用户数目，在本研究中将活跃用户数作为人口的代理(proxy)。我们从原始数据集中提取了两个子集，生成了两张人口分布时相数据，见图4。图4(a)为1月18日至1月22日，可看作在春节之前两周内一个普通工作周的日均人口分布；图4(b)为2月7日至2月11日（2月7日为除夕），可看作春节期间的日均人口分布。

 

   

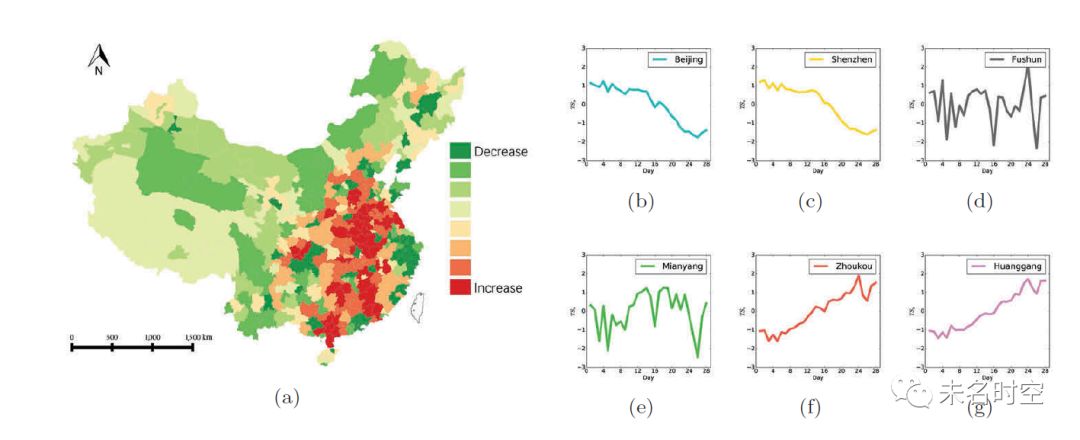
图 5 (a)春节前到春节期间的城市尺度人口数量变化 (b-g) 几个典型城市的标准化时谱曲线

    图5(a)可视化了空间分布演化的总体模式，而图5(b-f)则分别展示了北京、深圳、抚顺、绵阳、周口以及黄冈六个不同规模城市的人口演变时谱曲线。可以看出，核心省会城市的人口在春运期间呈现下降趋势，而小规模城市的人口趋势则各不相同。

 

   

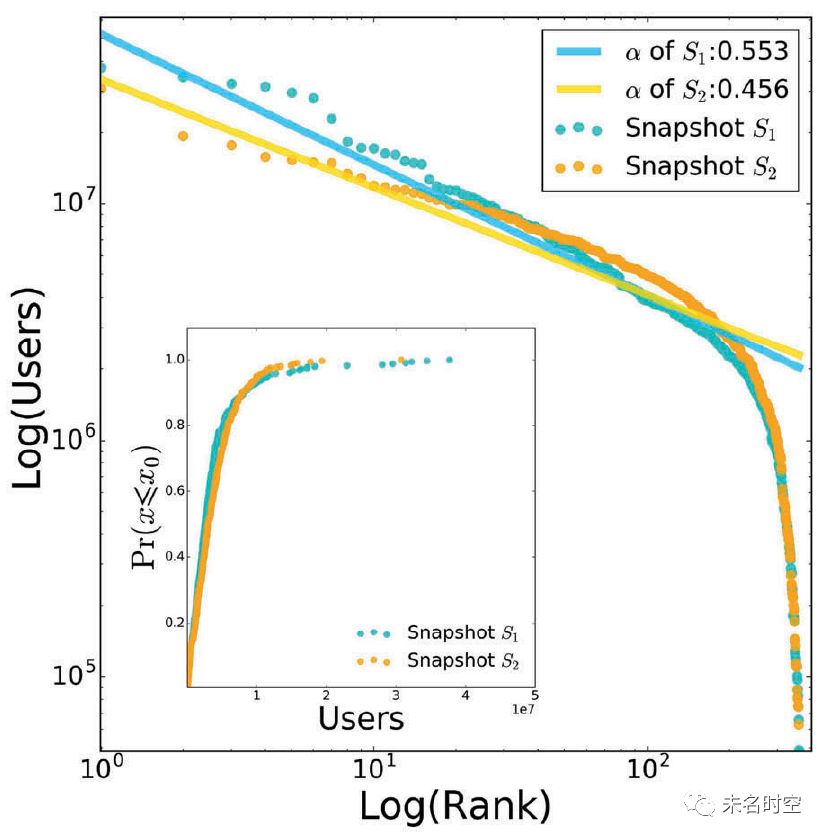
图 6 两个人口分布时相的位序规模比较

    图6将两个时相的城市人口位序规模分布（rank-size）进行了幂率拟合，幂指数α体现了人口分布的不均衡程度。S1的位序规模分布在双log坐标系下相较S2具有更陡的斜率（0.553>0.456），表明春节前的人口分布从空间相对聚集变得更加分散，证明了这期间的确存在着导致人口分布发生演化的宏观交互模式。这种模式需要本研究提出的IIDS方法进一步求解。

 

结果

 

   

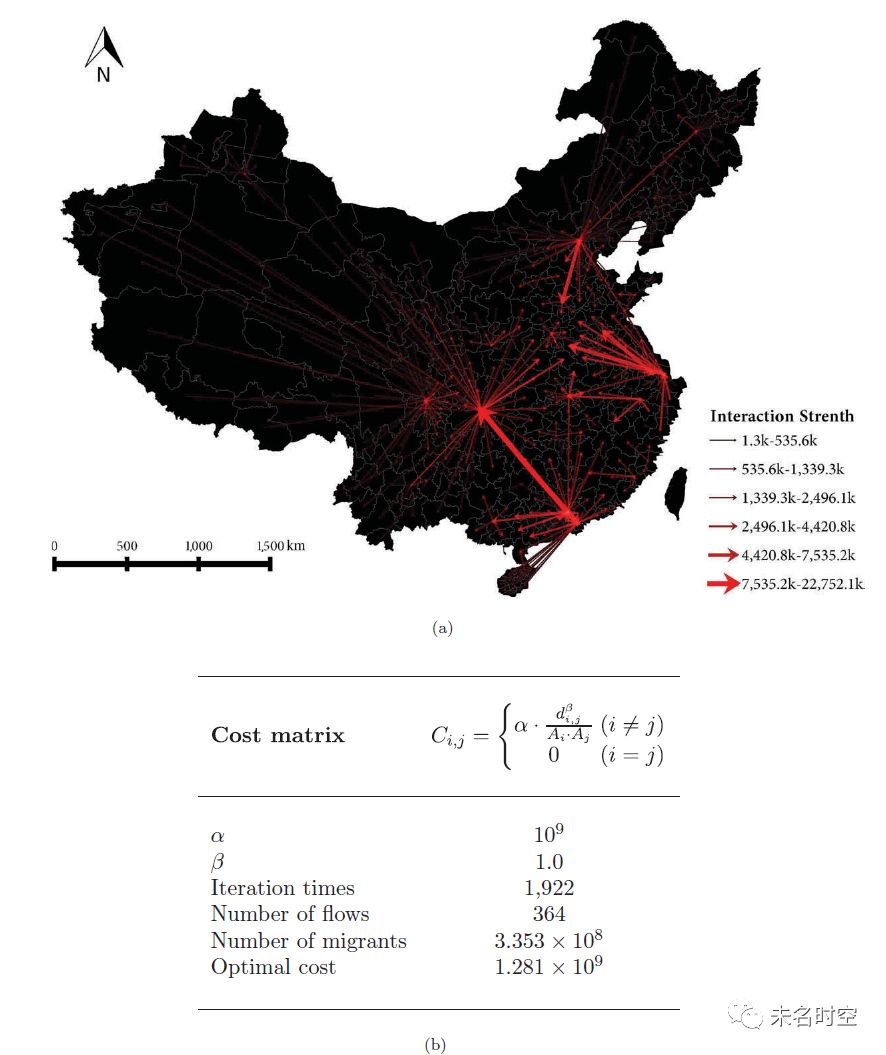
图 7 空间交互模式推算结果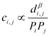（     ，β=1.0）

    交互成本矩阵采用基于重力模型的定义，β=1.0，我们的方法通过单纯形法迭代了1922次得到了最优的空间交互模式。共364个交互，包括超过3亿条个体移动，如图7所示，箭头的颜色的粗细反映了交互的强度（个体移动次数）。可以很容易地发现中国的四个主要城市群：长三角、珠三角、京津冀和成渝在春运中扮演着核心角色。大部分省会城市作为人流源头产生向省内附属城市迁移的交互。由于基于重力模型的成本定义，长距离的交互明显少于短距离的交互，而一些大城市之间的长距离交互也得以被发现，比如从深圳到重庆的返乡流（重庆具有大量在深圳务工的人员）。局部空间交互模式的细节如图8所示。

 

   

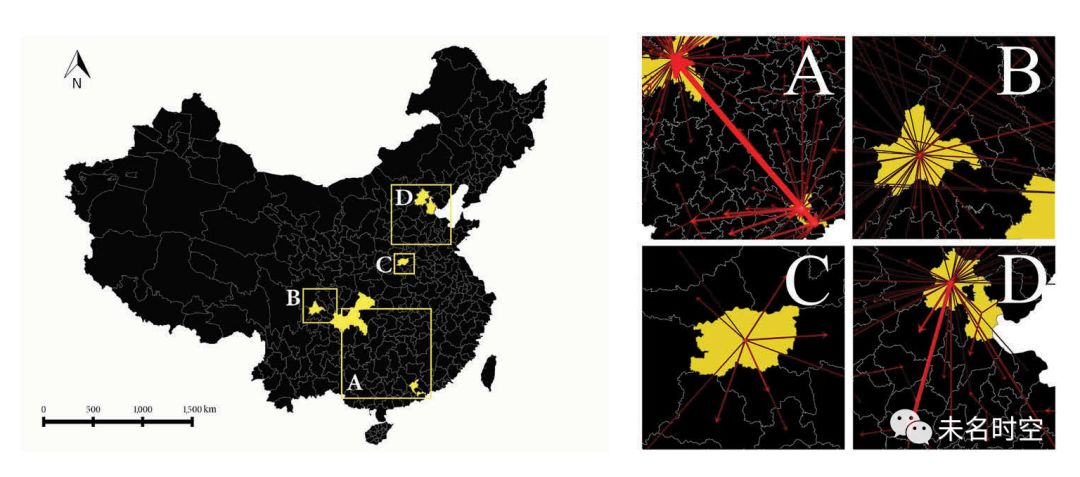
图 8 局部空间交互模式，A为重庆与珠江三角洲的长距离交互模式，B为成都市的省会辐射模式，C为郑州市的省会辐射模式，D为京津冀的区域交互模式

 

 

讨论

 

定量评估推算结果

   

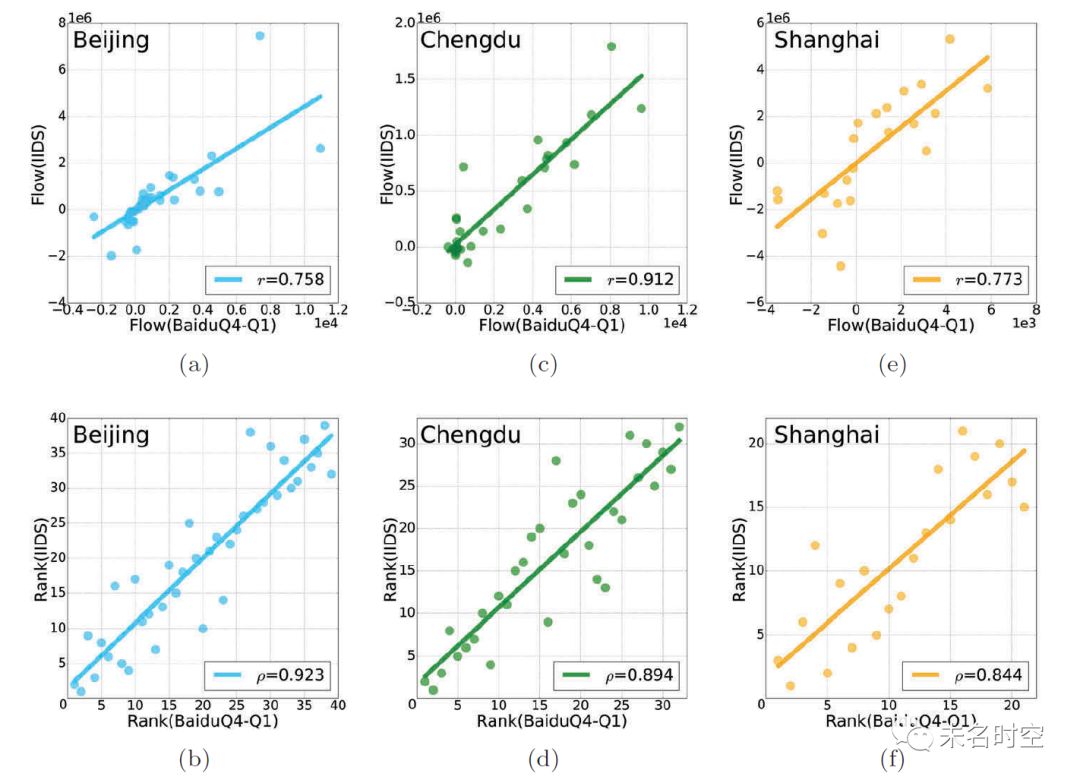
图 9 主要城市春运期间流推算结果与百度季度迁移数据（2015Q4到2016Q1）的相关性分析

 

    由于春运期间的真实人口迁徙数据无法获取，我们使用百度提供的从2015年第四季度到2016年第一季度的城市尺度人口迁移数据作为替代进行对图7结果的定量评估依据。我们对北京、成都和上海三个相对较大城市（交互模式相对稳定）的IIDS推算结果和对应的百度季度迁移数据进行相关性分析，如图9所示。图(a),(c),(e)回归得到交互强度的皮尔逊（Pearson）相关系数r，而图(b),(d),(f)回归得到交互强度位序的斯皮尔曼（Spearman）相关系数ρ。可以看出，基于重力成本矩阵，β=1.0的流推算结果与季度迁移真实数据呈现出高度的正相关关系（r>0.75,ρ>0.8）。考虑到两组数据的时间采样并非完全一致，图9的相关性分析足以说明方法的可行性。

 

关于成本矩阵的定义

    通过修改重力模型成本矩阵中距离衰减的β参数，可以对流推算的偏好进行微调。更高的β值代表着更强的距离阻隔效应，而更低的β值增加了长距离交互出现的概率，图10所示是β=0.8和0.4的推算结果。另外，图11展示了使用其他形式交互成本定义得到的推算结果，包括只考虑引力、只考虑距离和等成本的三种情况。具体的实证解读，请感兴趣的读者阅读原论文。

 

   

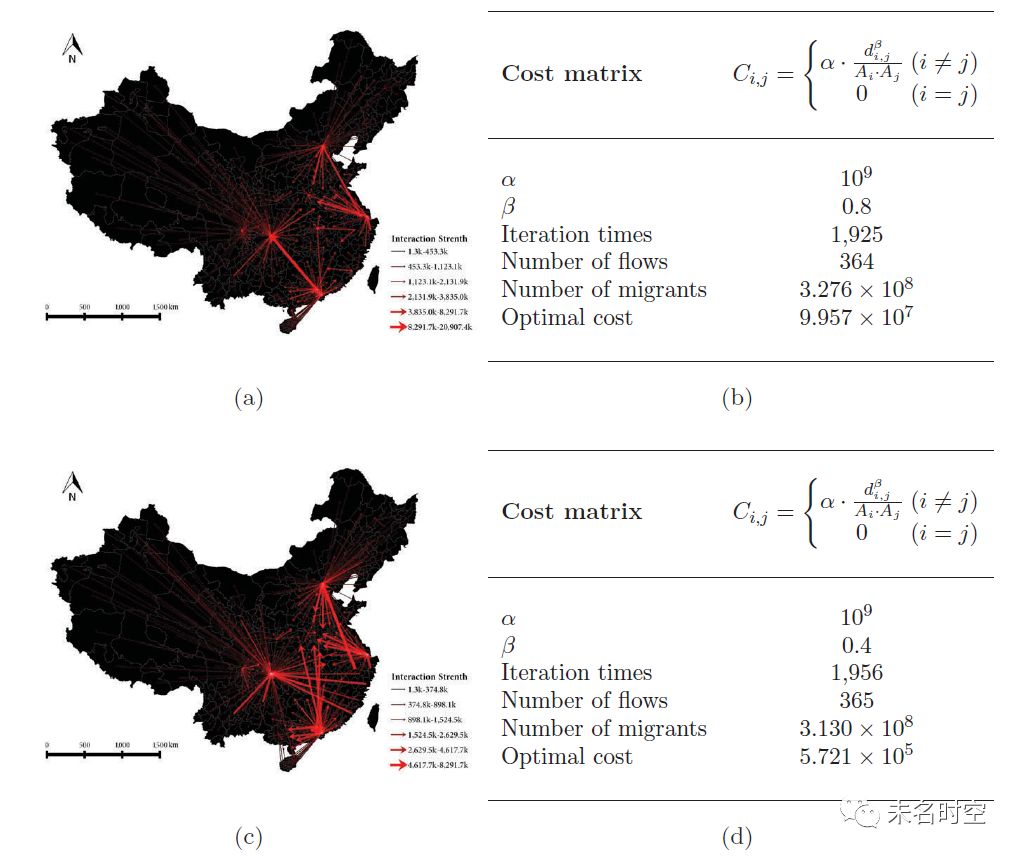
图 10 调整距离衰减参数后的空间交互模式推算结果

 

   

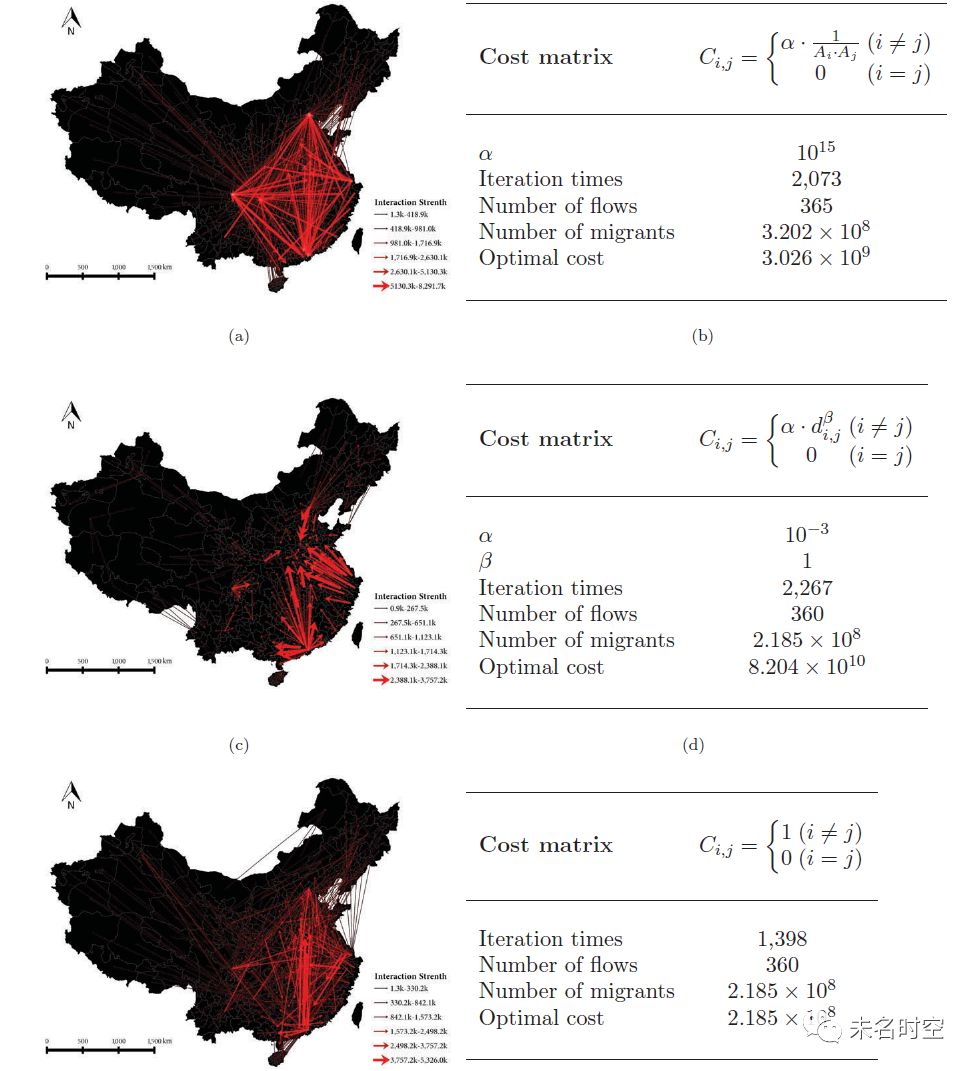
图 11 调整交互成本矩阵形式后的空间交互模式推算结果

 

 

结论

    连续空间分布快照数据所体现的空间演化过程受到空间交互的驱动。例如，在人口分布演化的背后隐藏的是人类的迁移流动(migration flow)。在大数据时代，我们能够较为轻松地得到高时空分辨率的分布数据，但想获取高质量的空间交互信息仍具有很大的挑战性。目前大部分研究着眼于描述分布特征或是对空间交互的建模，却少有工作尝试挖掘隐藏在分布演化背后的交互模式。通过将大规模线性规划算法（linear programming）以及人类移动的空间约束进行整合，我们提出了一种基于连续空间分布快照反演空间交互模式的方法，在提取2016年中国春节期间城际返乡流的实验中取得了理想的实证结果。本研究证明了利用离散多时相人口空间分布推算空间交互模式的可行性，为研究空间分异与空间交互之间的关系提供了新思路。

 

参考文献：Zhu, D., Huang, Z., Shi, L., Wu, L., & Liu, Y. (2017). Inferring spatial interaction patterns from sequential snapshots of spatial distributions. International Journal of Geographical Information Science, 1-23. DOI 10.1080/13658816.2017.1413192

素材来源：朱 递

材料整理：朱 递

内容编辑：龚旭日